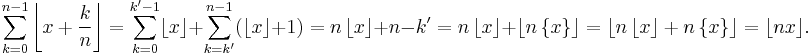Hermite's identity
In mathematics, the Hermite's identity states that for every real number x and positive integer n the following holds:
Proof
Write 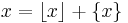 . There is exactly one
. There is exactly one  with
with
Now
In mathematics, the Hermite's identity states that for every real number x and positive integer n the following holds:
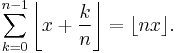
Write 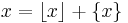 . There is exactly one
. There is exactly one  with
with
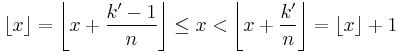
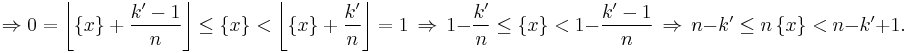
Now